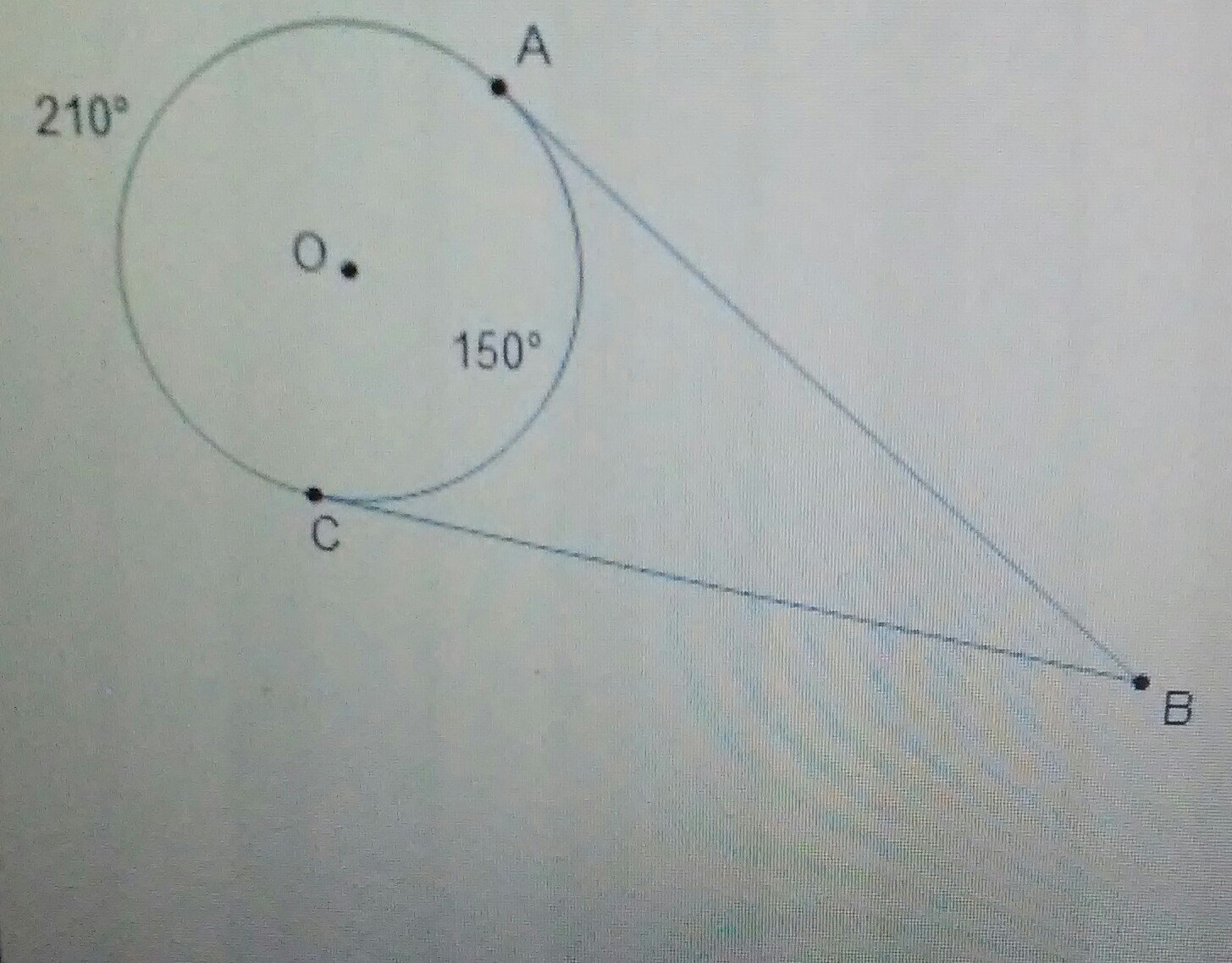
In the diagram of circle O, the measure of angle x is the central focus. Understanding this angle’s significance helps unravel the circle’s mysteries. By grasping the geometric properties at play, we can unlock its secrets with precision. Let’s delve into the depths of circle O and explore the fascinating realm of angles within its curved confines. Join the journey as we uncover the measure of x and illuminate the path to geometrical enlightenment.
In the Diagram of Circle O, What is the Measure Of?
Welcome, curious minds, to a fascinating journey into the world of circles and angles! Have you ever found yourself looking at a circle on a test or in a geometry problem and wondering about the mysterious measures within it? Well, you’re in the right place because today we are going to unravel the secrets of the diagram of circle O and discover just what is the measure of various angles within it. So, buckle up and let’s dive into the captivating world of circles!
The Basics of Circle Geometry
Before we delve into the specifics of the diagram of circle O, let’s establish some foundational knowledge about circles and angles. A circle is a perfectly round shape that is formed by all the points equidistant from a fixed point called the center. In the context of geometry, circles are full of interesting angles and measurements waiting to be explored!
Understanding Angles in a Circle
One of the key concepts when dealing with circles is understanding angles. In a circle, the measure of an angle is determined by the amount of rotation between its rays, with the center of the circle serving as the point of reference. There are several types of angles within a circle that we need to be familiar with:
- Central Angle: An angle whose vertex is at the center of the circle.
- Inscribed Angle: An angle formed by two chords in a circle that have a common endpoint.
- Interior Angle: An angle formed inside the circle by two chords or a chord and a tangent.
- Exterior Angle: An angle formed outside the circle by extending one side of a triangle.
Exploring the Diagram of Circle O
Now that we have a good grasp of the basic concepts, let’s turn our attention to the intriguing diagram of circle O. In this diagram, we will encounter various angles that hold the key to unlocking the mysteries of circle geometry. Let’s take a closer look at some of the angles you might encounter in circle O:
Measure of Central Angle
One of the fundamental angles in a circle is the central angle. This angle is formed by two radii extending from the center of the circle to any point on its circumference. The measure of a central angle is directly related to the arc it intercepts. In the diagram of circle O, the measure of a central angle can be calculated using a simple formula: the measure of the central angle is equal to the measure of its intercepted arc.
For example, if the central angle in circle O intercepts an arc of 60 degrees, then the measure of the central angle is also 60 degrees. Central angles play a crucial role in understanding the relationships between angles and arcs within a circle.
Finding the Inscribed Angle Measure
Another interesting angle to explore in the diagram of circle O is the inscribed angle. An inscribed angle is formed by two chords in a circle that have a common endpoint on the circle’s circumference. The measure of an inscribed angle is half the measure of its intercepted arc.
Imagine a scenario in circle O where an inscribed angle intercepts an arc of 120 degrees. In this case, the measure of the inscribed angle would be half of 120 degrees, which is 60 degrees. Inscribed angles provide valuable insights into the geometry of circles and are essential in solving various problems involving circles.
Unraveling the Mystery of Interior and Exterior Angles
Interior and exterior angles in a circle add another layer of complexity to our exploration. Interior angles are formed inside the circle by two chords or a chord and a tangent, while exterior angles are formed outside the circle by extending one side of a triangle.
In the diagram of circle O, interior angles can help us determine relationships between various elements of the circle, such as chords and tangents. Understanding interior angles allows us to analyze the interactions between different components of the circle and make predictions about their properties.
On the other hand, exterior angles in circle O provide insights into how triangles can be formed using the circle as a reference point. By extending one side of a triangle outside the circle, we can observe the relationships between the angles and sides of the triangle and how they connect to the circle.
Putting It All Together
As we journey through the diagram of circle O and uncover the measures of various angles within it, we start to see the intricate connections between angles, arcs, and lines in circle geometry. By mastering the concepts of central angles, inscribed angles, interior angles, and exterior angles, we gain a deeper understanding of the properties and relationships that exist within a circle.
So, the next time you come across a circle in your math homework or a geometric problem, remember the lessons learned from exploring the diagram of circle O. With a keen eye and a curious mind, you can decipher the measure of angles within the circle and unlock the secrets of its geometry.
Keep exploring, keep learning, and let the wonders of circle geometry guide you on your mathematical journey!
Thank you for joining us on this enlightening adventure into the world of circles and angles. Until next time, happy exploring!
In the diagram of circle O, what is the measure of ∠ABC? 27° 54° 108° 120° B A 126° 0°, 234…
Frequently Asked Questions
What is the measure of angle x in circle O?
The measure of angle x in circle O is equal to half the measure of the intercepted arc it subtends. Therefore, to find the measure of angle x, you need to know the measure of the intercepted arc.
How do you find the measure of an angle in the diagram of circle O?
To find the measure of an angle in the diagram of circle O, you can use the central angle theorem. This theorem states that the measure of a central angle is equal to the measure of the intercepted arc it subtends. So, by knowing the measure of the intercepted arc, you can determine the angle’s measure.
Can you explain how to calculate the measure of angle y in circle O?
To calculate the measure of angle y in circle O, you need to consider the relationship between the inscribed angle and the intercepted arc. The measure of an inscribed angle is half the measure of the intercepted arc it subtends. Therefore, by knowing the measure of the intercepted arc, you can find the measure of angle y.
Final Thoughts
In the diagram of circle o, what is the measure of ∠ABC? The angle ∠ABC measures 90 degrees, forming a right angle at point B. This angle is crucial for understanding the relationships within circle o. Remember, the measure of ∠ABC is essential when solving geometric problems related to circle o. Always pay attention to this angle when analyzing circle diagrams.